- Pythonの「numpy」ライブラリで「どうにかfor文を減らせないか」という人に向けた記事です。
- ブロードキャストとeinsumを使う方法を紹介します。
pythonではforループで計算を回すと遅いという特徴があります。
よく知られているようにnumpyをうまく使うのがポイントです。
このnumpyがクセがあり分かりづらいので、忘備録としてまとめます。
計算
2次元x2次元 = 3次元の計算
二つの行列の積から3次元データを生成します。(この積の名前は何でしょうか?)
z[i,j,k]= x[i,j] * y[i,k]
図で書けばこんな感じです。

コード例
import time
import numpy as np
si,sj,sk = 2, 5000, 500
# 適当に計算値を用意
x = np.reshape(np.arange(si*sj),(si,sj))
y = np.reshape(np.arange(si*sk),(si,sk))
# C文の場合
start = time.time()
z = np.empty((si,sj,sk))
for k in range(sk):
for j in range(sj):
for i in range(si):
z[i,j,k] = x[i,j] * y[i,k]
process_time = time.time() - start
print(f"for loop: {process_time}")
# numpyブロードキャストの場合
start = time.time()
z = x[:,:,np.newaxis] * y[:,np.newaxis,:]
process_time = time.time() - start
print(f"broadcasting: {process_time}")
# numpy einsumの場合
start = time.time()
z3 = np.einsum("ij,ik->ijk",x,y)
process_time = time.time() - start
print(f"einsum: {process_time}")Google colabで試すと、for文より500倍くらい速いですね。
for loop: 5.083636999130249
broadcasting: 0.008948802947998047
einsum: 0.009719133377075195解説
3重forループ
z = np.empty((si,sj,sk))
for k in range(sk):
for j in range(sj):
for i in range(si):
z[i,j,k] = x[i,j] * y[i,k]1つ目は3重forループです。速度はともかく中身はわかりやすいです。
numpyのブロードキャスト
z = x[:,:,np.newaxis] * y[:,np.newaxis,:]2つ目はnumpyのブロードキャストです。
多次元データのブロードキャストには、長さが1の新しい軸を追加する必要があります。図で描くとこんな感じ。
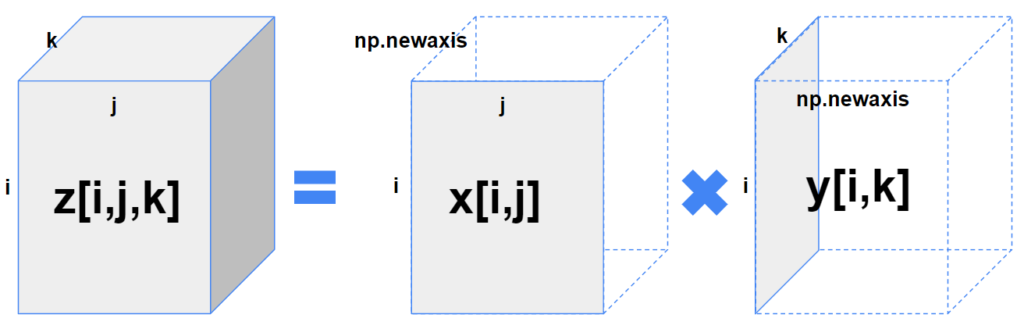
xに3軸目を追加し、yには2軸目を挿入することでブロードキャストが可能になります。
numpyでは「np.newaxis」で長さ1の新しい軸を作成できますので、それぞれx[:,:,np.newaxis]とy[:,np.newaxis,:]とすればOKです。
※ np.newaxisの実態は「None」なので、ただNoneと書いてもOKです。
z = x[:,:,None] * y[:,None,:]ブロードキャストは便利なのですが動作がわかりにくくいので、後から理解しやすいようにコメント付けておくと良いですね。
自分で見返したときにわからない!なんてことはよくあります。
自分はnumpyのブロードキャストは下記の書籍で知りました。
紙の本は検索できないのは不便ですが、何となく読むのには意外と良かったりしますよね。
numpy einsum
z3 = np.einsum("ij,ik->ijk",x,y)3つめはnumpyのeinsumです。多次元データの積、和を柔軟に表現できます。
こちらは公式のリンクです。
- x 0次元目の長さi, 1次元目の長さj
- y 0次元目の長さi, 1次元目の長さk
から - z 0次元目の長さi, , 1次元目の長さj, 2次元目の長さk
を生成するので
“ij,ik->ijk”
になります。(はじめ分かりにくいかも知れませんが、まさにこの通りです。)
便利なので慣れてくると何でもこれで書きたくなります。
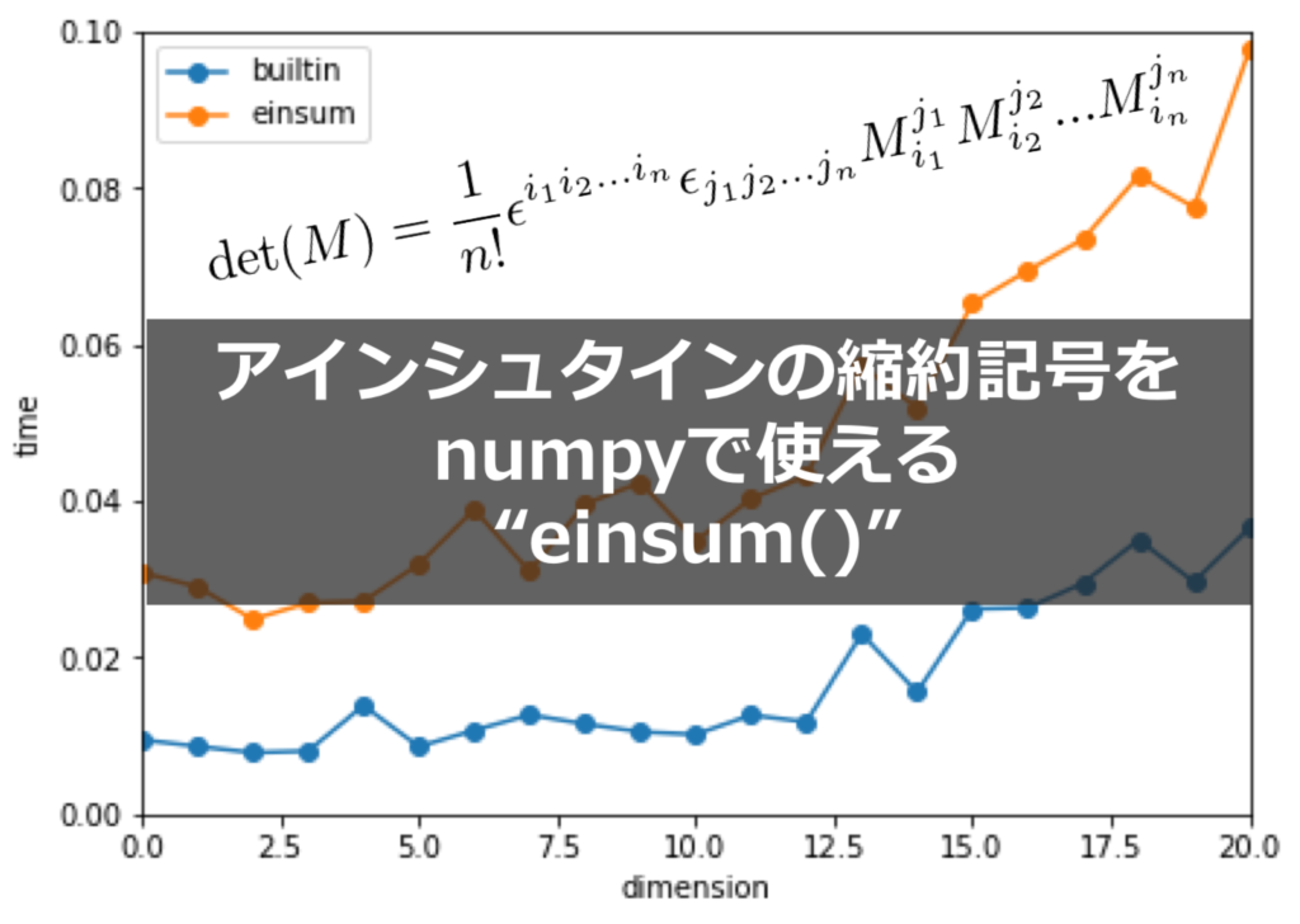
np.dotなどが速い場合もあるみたいなので、書きやすさ、メモリ、速度の兼ね合いで選ぶことになります。検索すると色々出てきますね。
まとめ
普段便利なpythonですが、クセがあるの行列計算の書き方です。numpyに慣れる書き方をご紹介しました。













コメント